PROGRAM KEAHLIAN : AKUNTANSI DAN PEMASARAN
TAHUN PELAJARAN 2012/2013
1. Seorang
peternak mempunyai persediaan pakan untuk 75 ekor kambing yang cukup
untuk 24 hari. Jika 3 ekor kambing hilang, maka persediaan pakan cukup
untuk ….
A. 28 hari
B. 27 hari
C. 26 hari
D. 25 hari
E. 22 hari
2. Sebuah
notebook dibeli dengan harga Rp3.000.000,00. Setelah 1 minggu dijual
dengan harga Rp2.760.000,00, maka persen rugi dari penjualan tersebut
adalah….
A. 6%
B. 7%
C. 8%
D. 9%
E. 12%
3. Jika x dan y merupakan penyelesaian dari sistim persamaan linier 2x – 3y = 5 dan 3x – 5y = 9. Nilai 5x – 3y = ....
A. 21
B. 19
C. 9
D. –1
E. –3
4. Himpunan penyelesaian dari pertidaksamaan kuadrat 3x
 6 – 7x dengan x
6 – 7x dengan x  R adalah ....
R adalah ....
D. { x ׀ x 
 atau x
atau x  3, x
3, x R}
R}
E. { x ׀ x  – 3 atau x
– 3 atau x 
 , x
, x R}
R}
5. Sinta
mempunyai uang Rp750.000,00, ia membeli 2 celana dan 3 kemeja uangnya
lebih Rp. 100.000,00. Jika ia membeli 4 celana dan 3 kemeja uangnya
kurang Rp100.000,00. Berapa banyaknya celana dan kemeja yang harus ia
beli agar uangnya cukup ?
3 celana dan 4 kemeja
3 celana dan 3 kemeja
3 celana dan 4 kemeja
4 celana dan 4 kemeja
5 celana dan 3 kemeja
6. Diketahui matriks K = 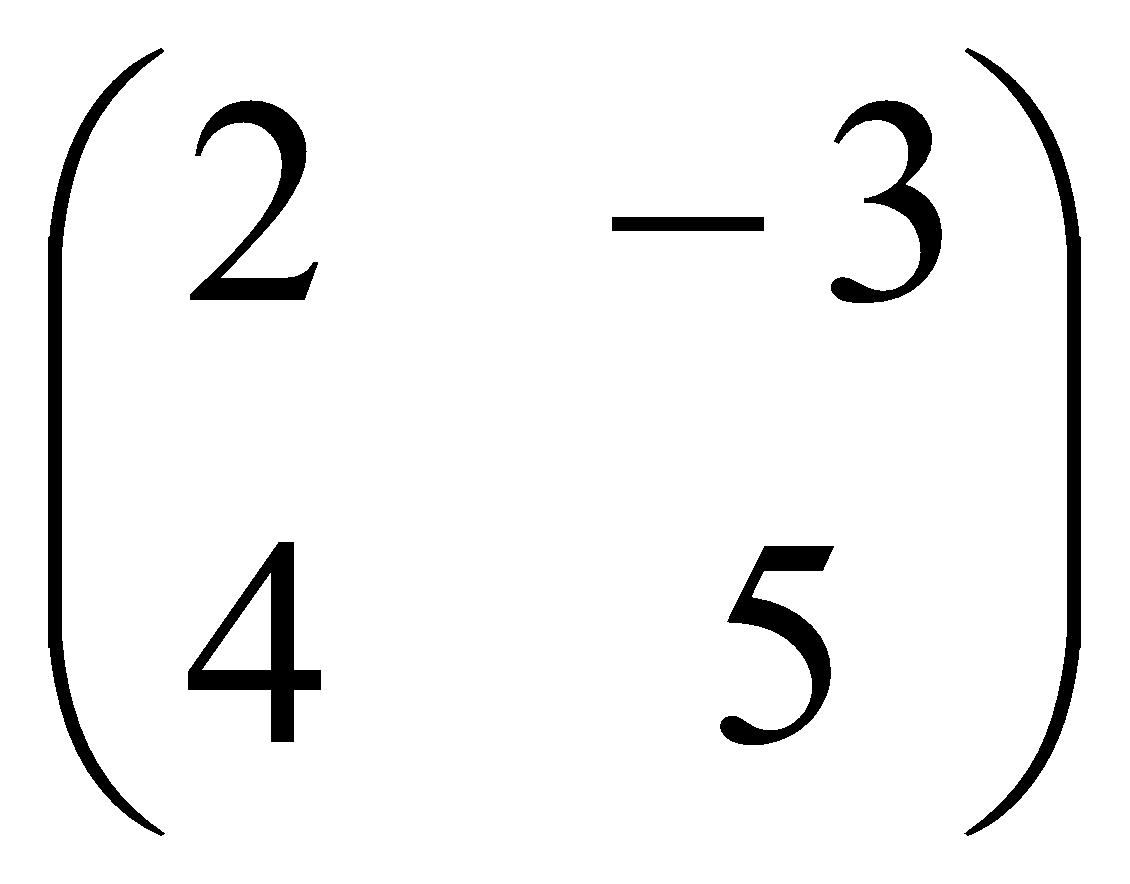 dan L =
dan L = . Matriks KxL = ....
. Matriks KxL = ....
A. 
B. 
C. 
D. 
E. 
7. Diketahui matriks A =  , maka A
, maka A = ....
= ....
A. 
B. 
C. 
D. 
E. 
8. Seorang
pemborong pengecatan rumah mempunyai persediaan 90 kaleng cat warna
putih dan 65 kaleng cat warna biru. Pemborong tersebut mendapat tawaran
untuk mengecat ruang tamu dan ruang tidur. Setelah dihitung ternyata
ruang tamu memerlukan 1,5 kaleng cat putih dan 2 kaleng cat biru.
Sedangkan ruang tidur memerlukan 2 kaleng cat warna putih dan 1,5 kaleng
cat warna biru. Jika banyaknya ruang tamu dinyatakan dengan x dan ruang
tidur dengan y, maka model matematika dari permasalahan di atas adalah
….
A. 3x + 4y 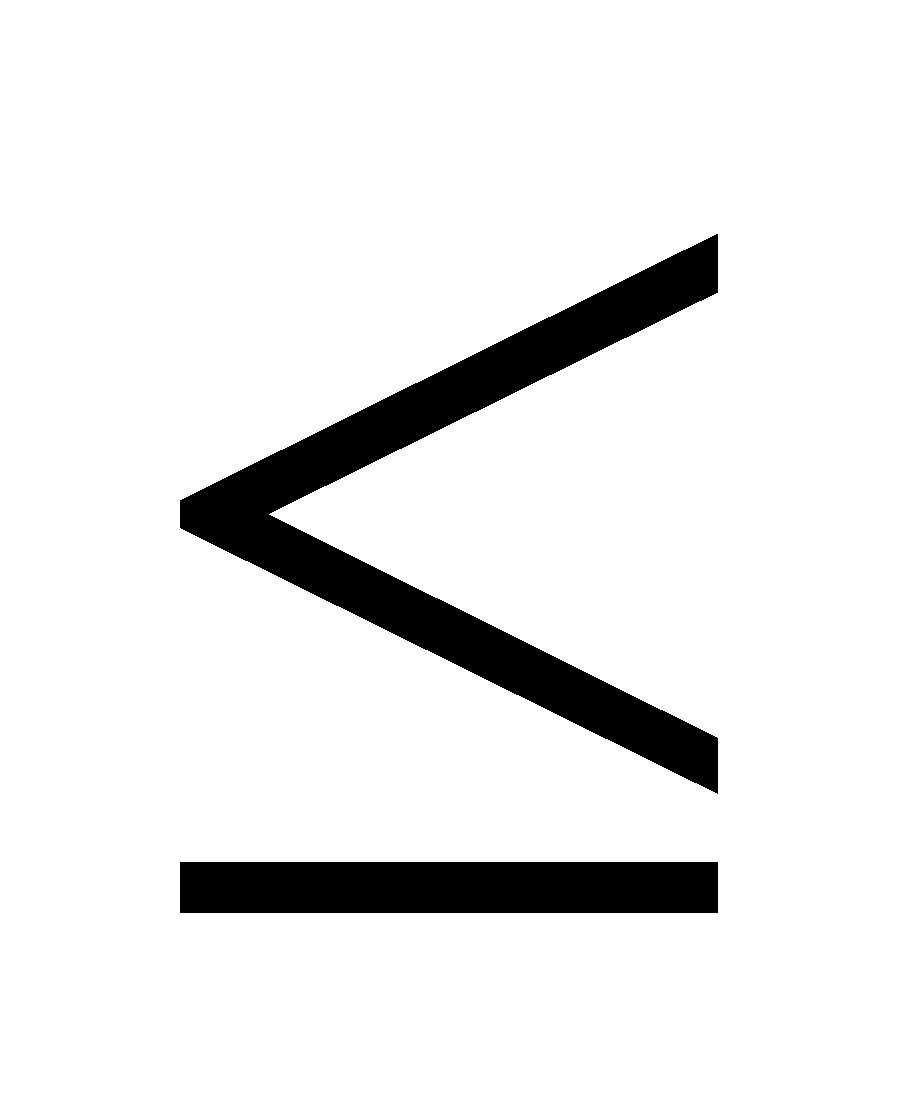 180; 4x + 3y
180; 4x + 3y  130; x
130; x  0; y
0; y  0
0
B. 3x + 4y 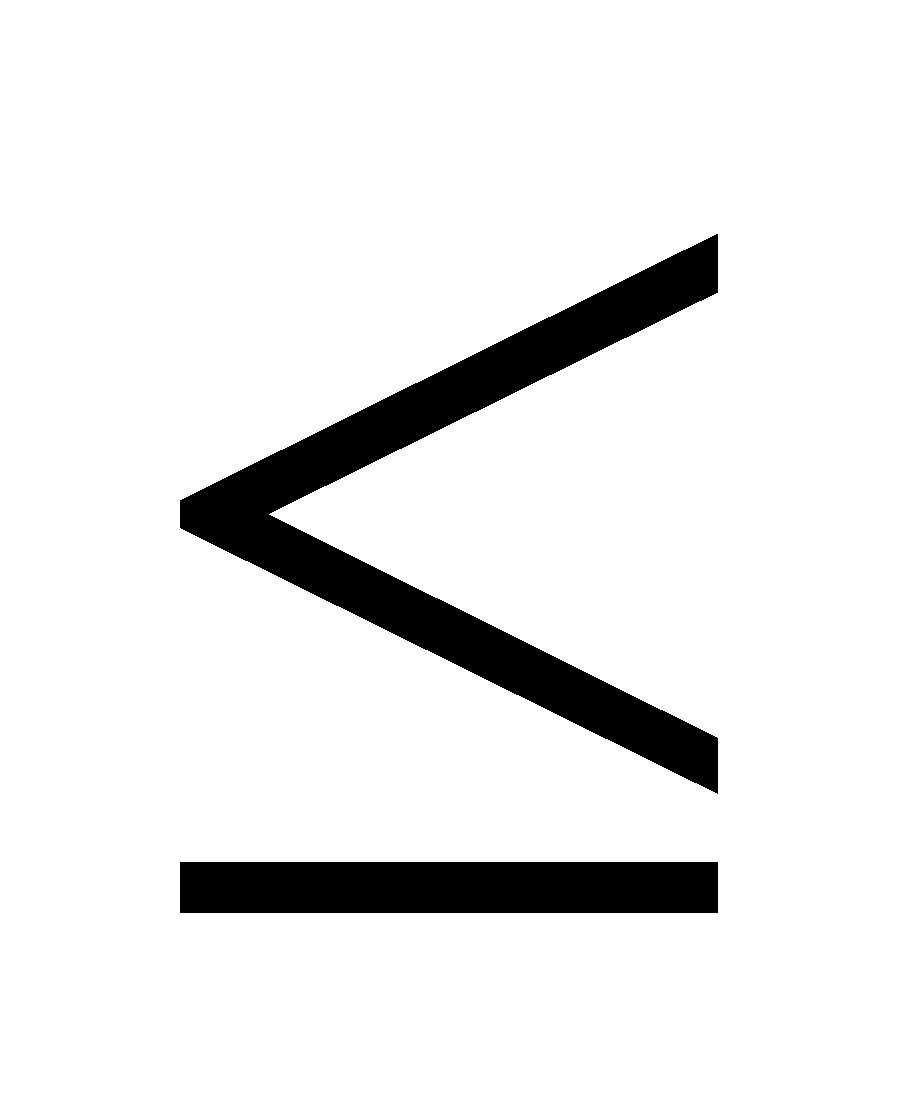 180; 3x + 4y
180; 3x + 4y  130; x
130; x 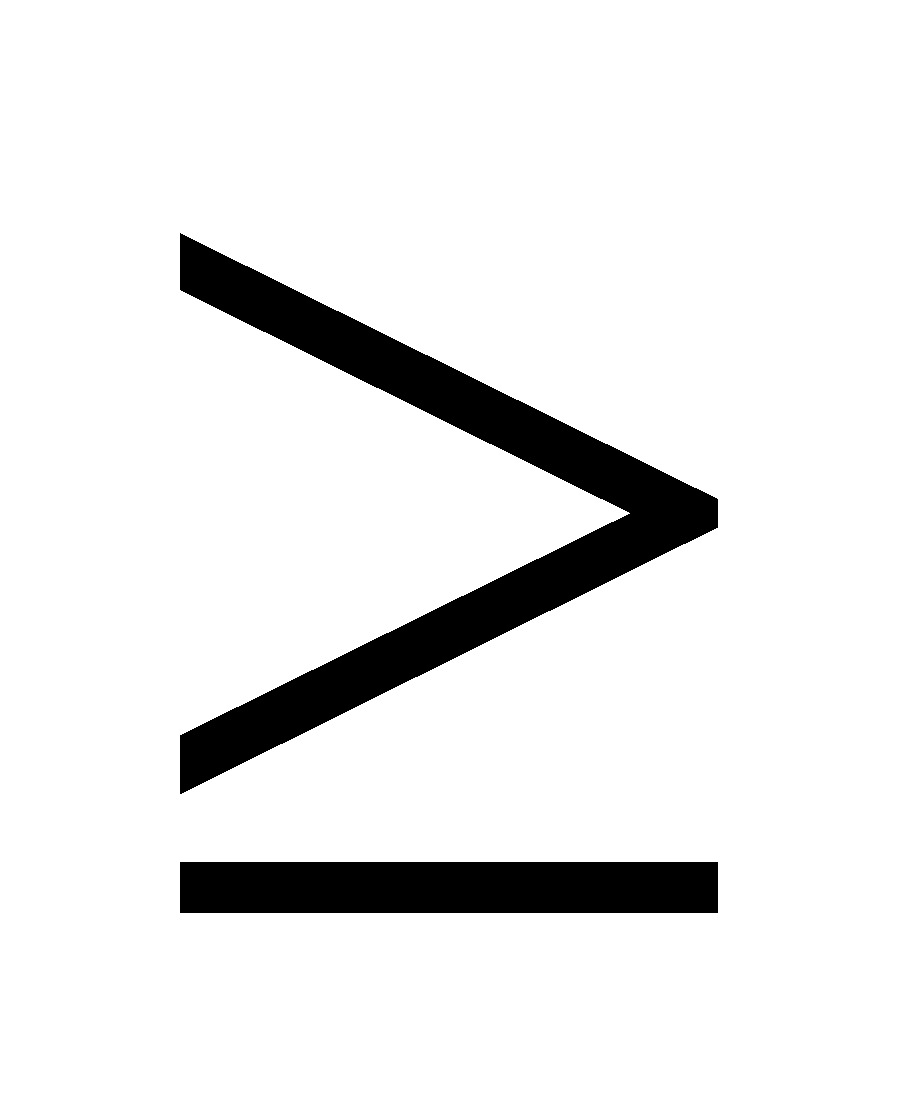 0; y
0; y  0
0
C. 4x + 3y 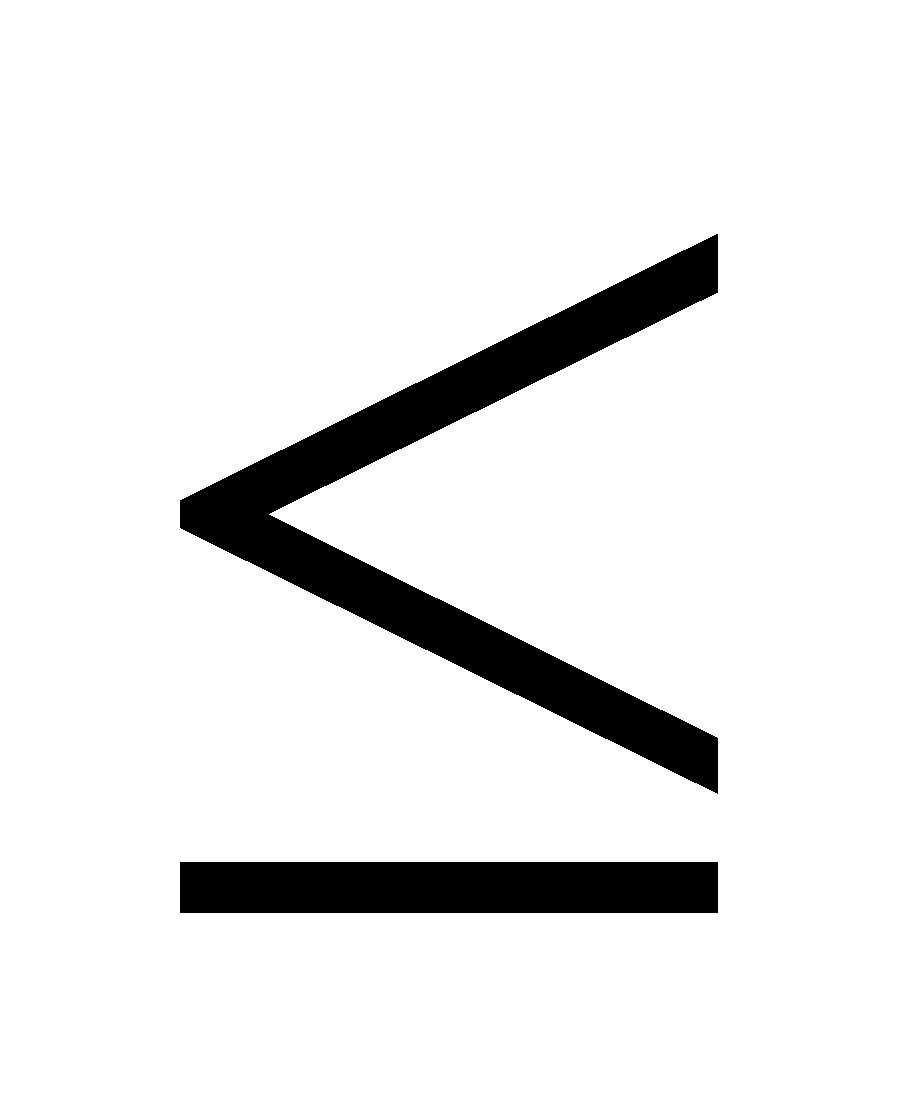 180; 3x + 4y
180; 3x + 4y  140; x
140; x 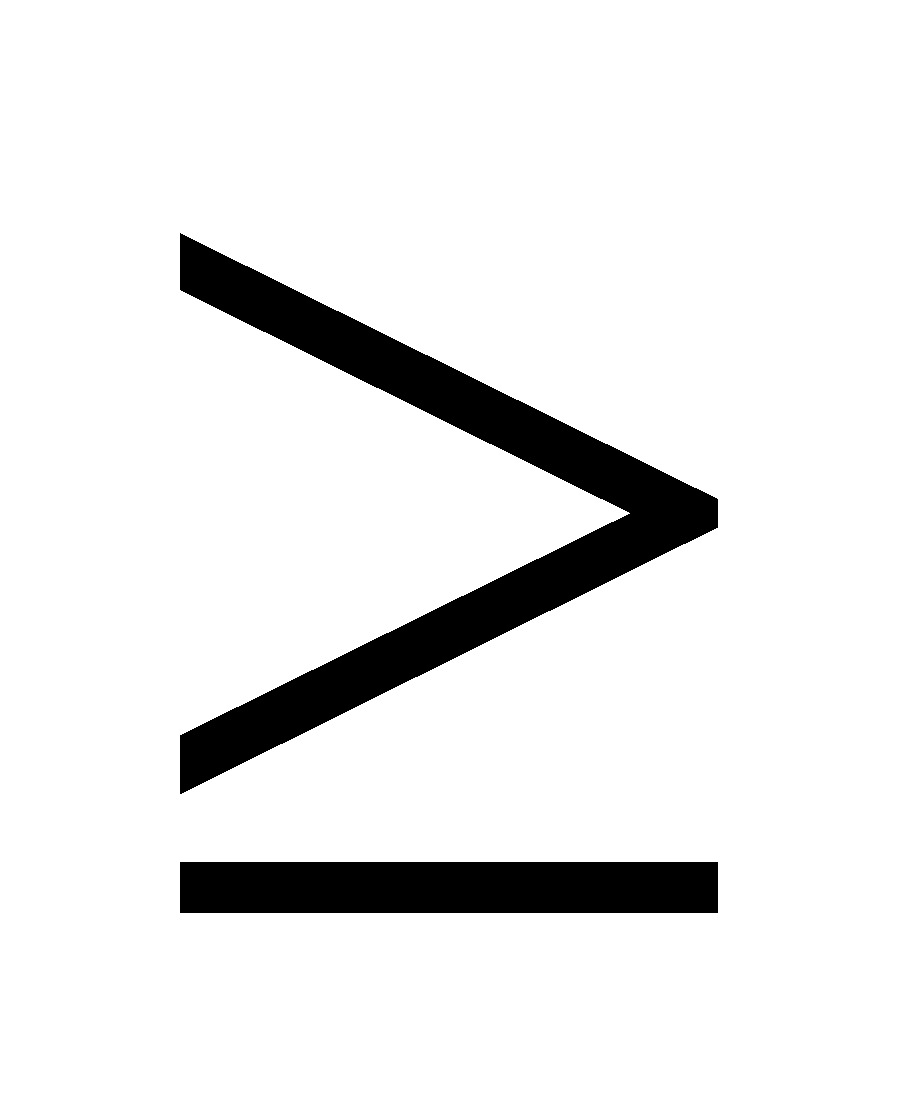 0; y
0; y  0
0
D. 4x + 3y 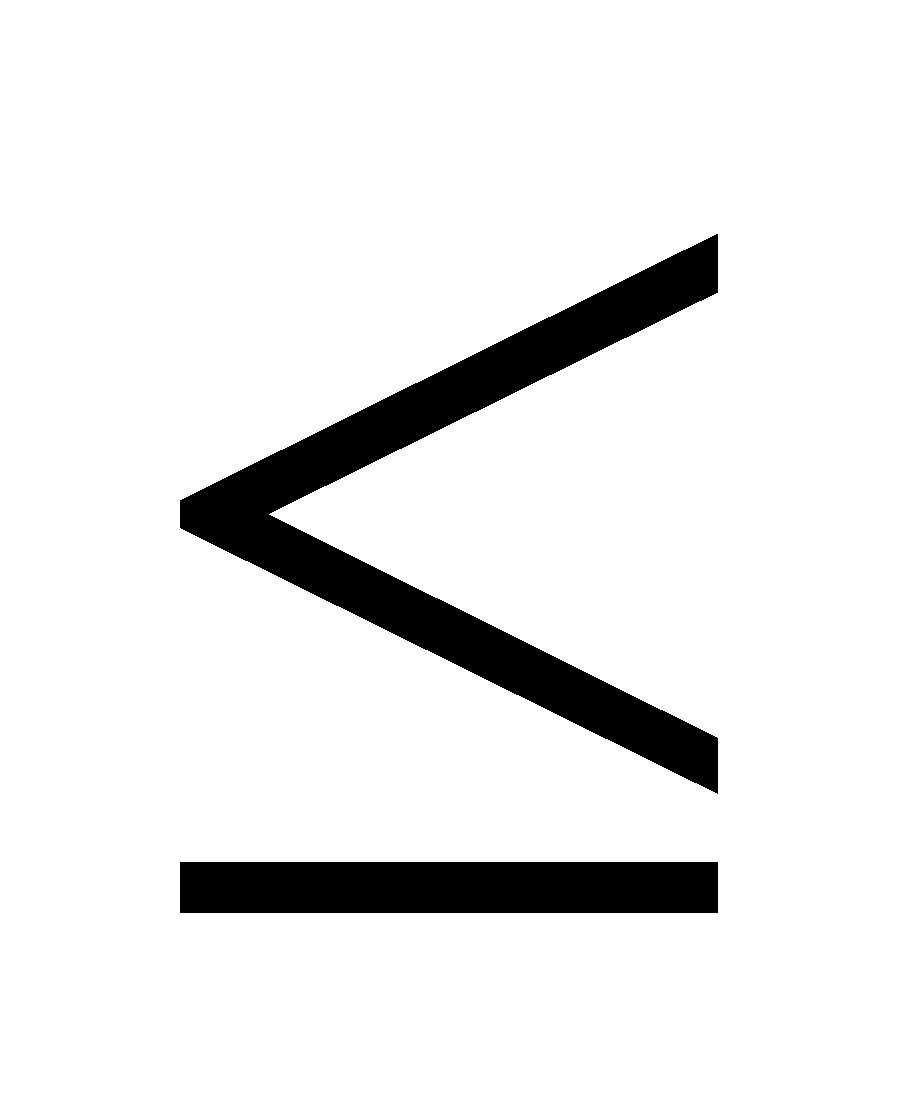 180; 3x + 4y
180; 3x + 4y  130; x
130; x 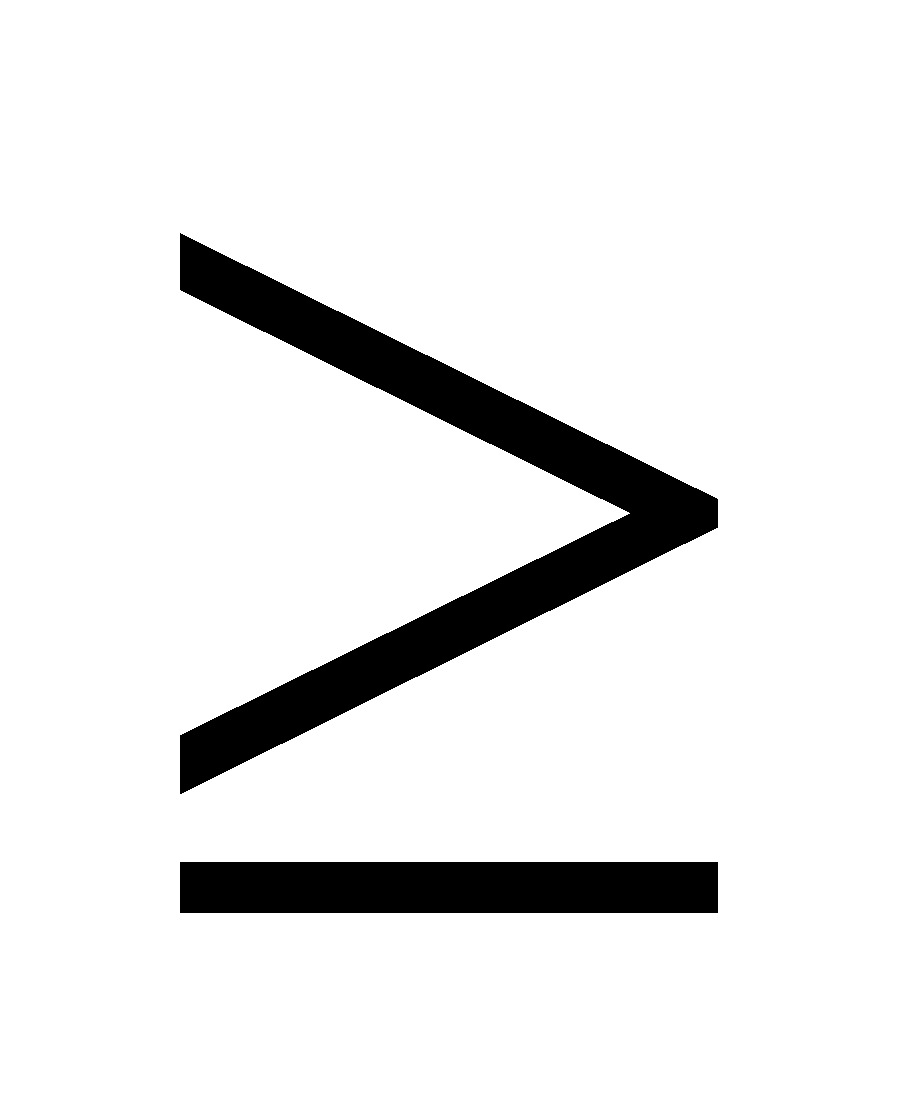 0; y
0; y  0
0
E. 4x + 3y 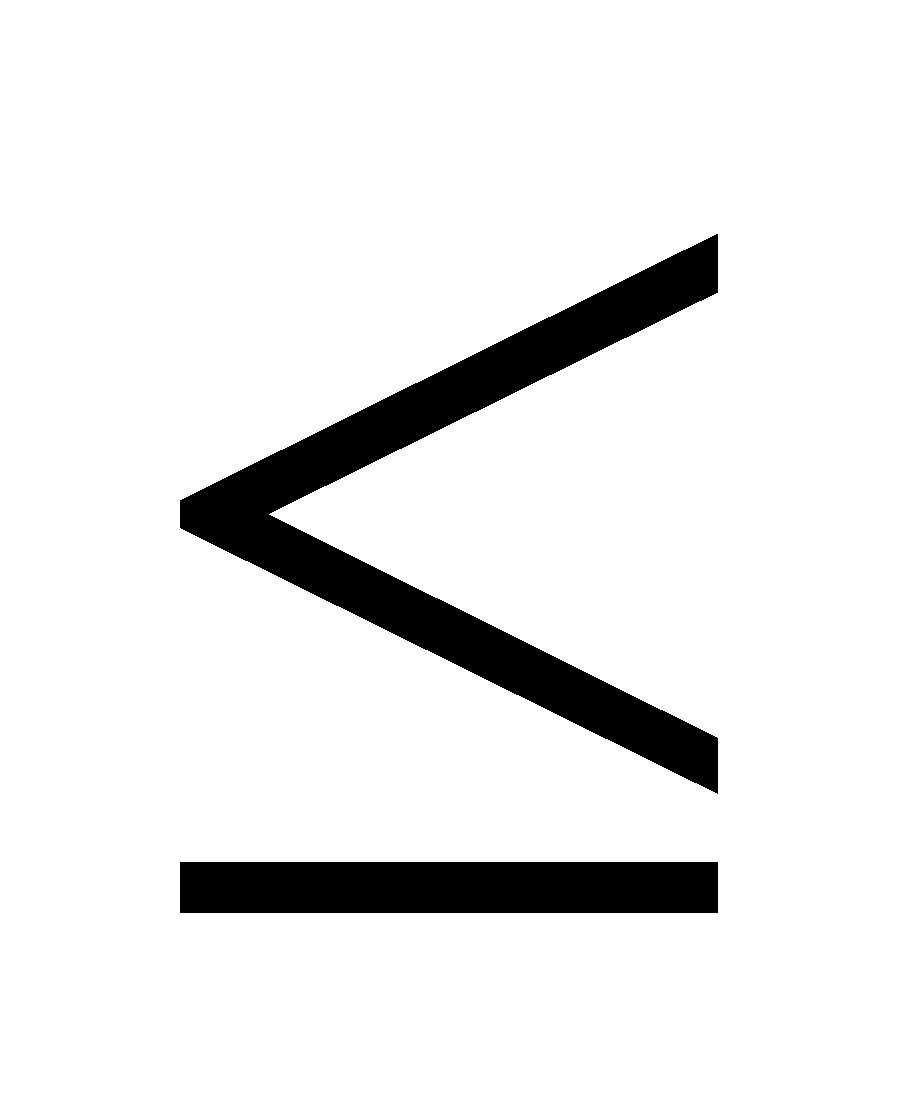 190; 3x + 4y
190; 3x + 4y  130; x
130; x 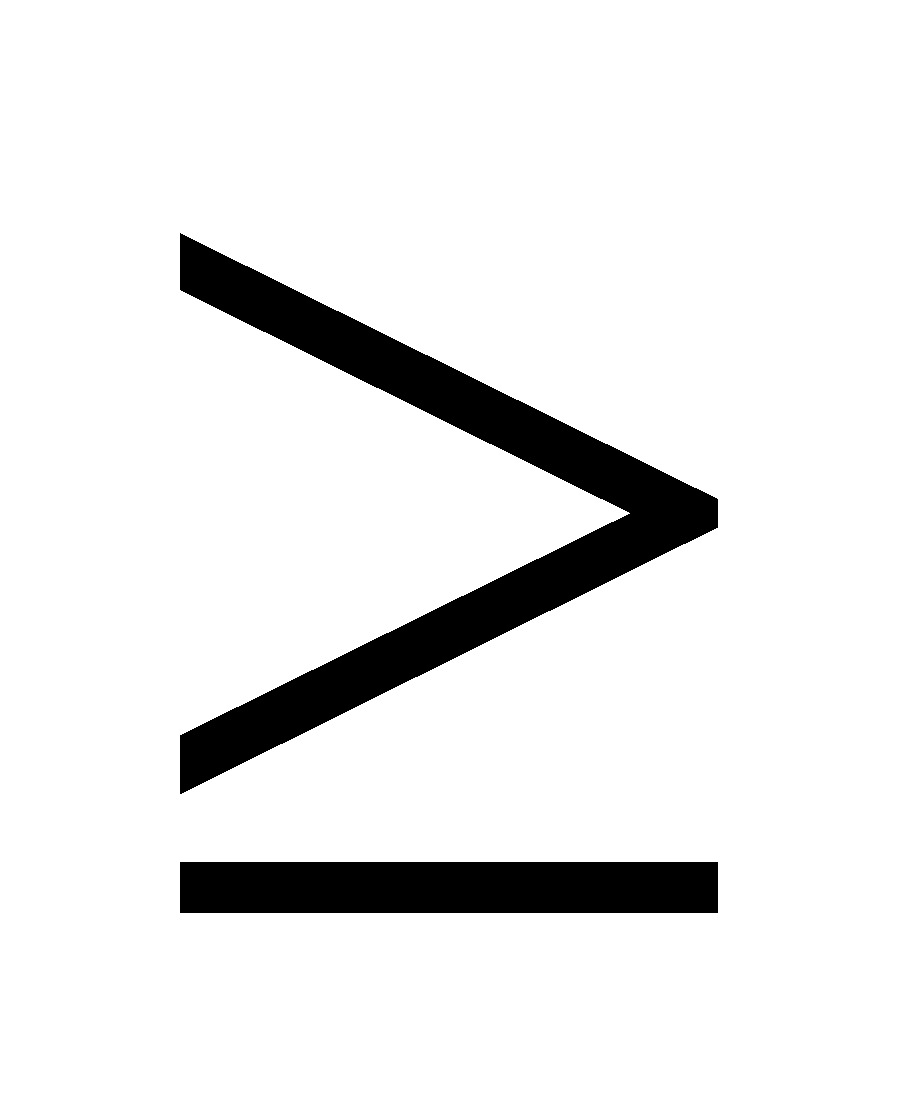 0; y
0; y  0
0
9. “Jika jalan diperbaiki maka perekonomian daerah akan berkembang”, negasi dari pernyataan tersebut adalah ….
A. Jalan diperbaiki atau perekonomian daerah tidak akan berkembang
B. Jalan diperbaiki dan perekonomian daerah akan berkembang pesat
C. Jalan diperbaiki dan perekonomian daerah sedikit berkembang
D. Jalan diperbaiki tetapi perekonomian daerah akan lebih berkembang
E. Jalan diperbaiki tetapi perekonomian daerah tidak akan berkembang
10. Diberikan premis – premis berikut :
Premis 1 : Jika volume tabung tiga kali volume kerucut maka nilai 


Premis 2 : nilai  =
=
Kesimpulan yang sah dari premis-premis di atas adalah …
B. Volume tabung tiga kali volume kerucut
C. Volume tabung bukan tiga kali volume kerucut
D. Volume tabung tiga kali volume kerucut dan nilai 


E. Volume tabung bukan tiga kali volume kerucut dan nilai 


11. Fungsi permintaan suatu barang dinyatakan dengan persamaan D : 2p = 3q + 10
dan fungsi penawaran S : 2q = 160 – 2p. Apabila p menyatakan harga barang dan
q menyatakan jumlah barang maka titik keseimbangan pasar terjadi pada ....
A. ( 30 , 40 )
B. ( 30 , 50 )
C. ( 40 , 30 )
D. ( 50 , 30 )
E. ( 50 , 60 )
12. Cermati grafik berikut!
Persamaan fungsi kuadrat yang memenuhi grafik di atas adalah ….
A. y = 2x + 8x +5
+ 8x +5
B. y = 2x - 8x +5
- 8x +5
C. y = 2x + 4x +5
+ 4x +5
D. y = x + 4x +5
+ 4x +5
E. y = x + 8x +5
+ 8x +5
13. Diketahui suku-suku barisan -50, -47, -44, -41, …, rumus umum barisan tersebut adalah ….
A. 
B. 
C. 
D. 
E. 
14. Empat suku pertama barisan yang ditentukan oleh rumus umum barisan  =
=  , adalah ….
, adalah ….
A. 3, 9, 19, 30
B. 3, 9, 19, 33
C. 3, 9, 19, 37
D. 3, 9, 19, 39
E. 3, 9, 19, 41
15. Diketahui suku-suku barisan aritmetika 6, 11, 16, …, 306. Banyaknya suku barisan tersebut adalah ….
A. 61 suku
B. 60 suku
C. 56 suku
D. 51 suku
E. 50 suku
16. Jika A =  , B
, B  , dan C =
, dan C = 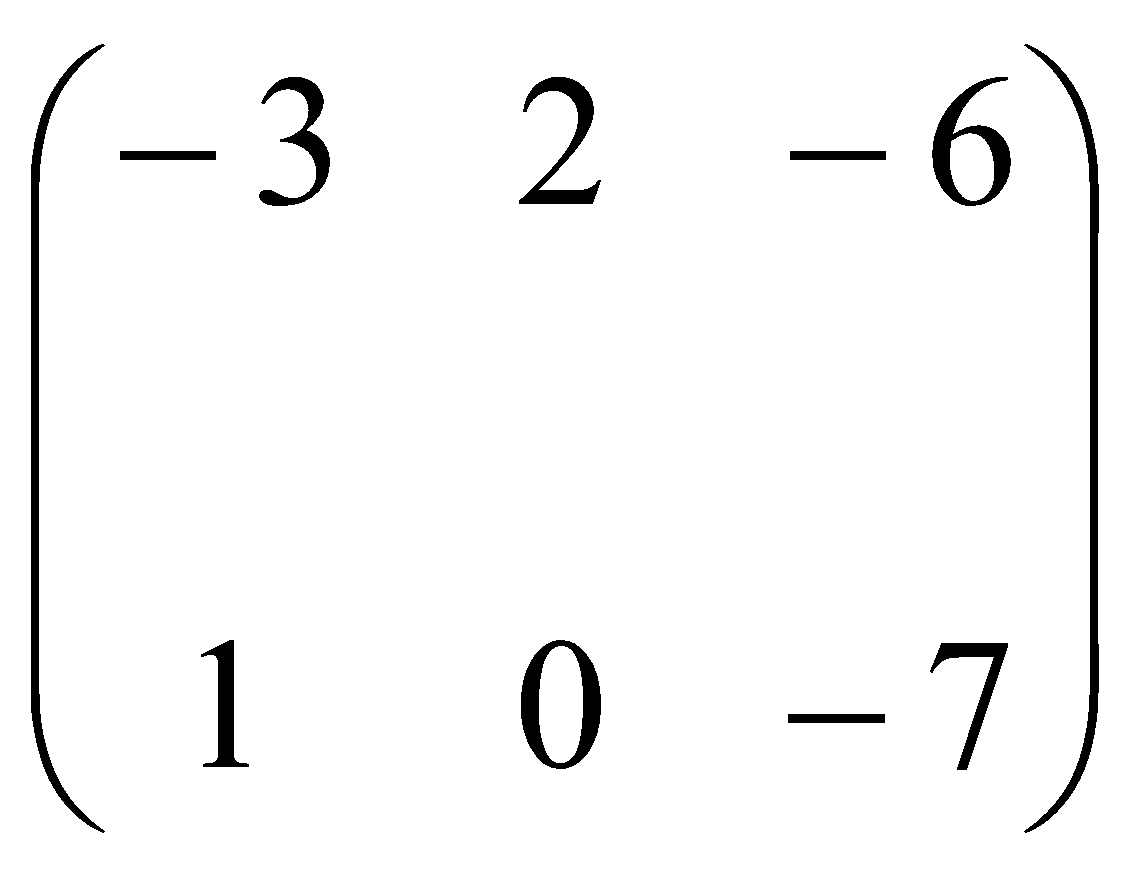 , maka 2A
, maka 2A
+ 3B – 4C = ….
-
-
-
-
-
17. Jumlah sampai suku tak hingga dari suatu deret geometri = 27. Apabila rasionya  , maka suku pertama deret tersebut adalah ….
, maka suku pertama deret tersebut adalah ….
A. 9
B. 12
C. 18
D. 54
E. 81
18. Sebuah bola jatuh dari ketinggian 8 meter dan memantul dengan ketinggian 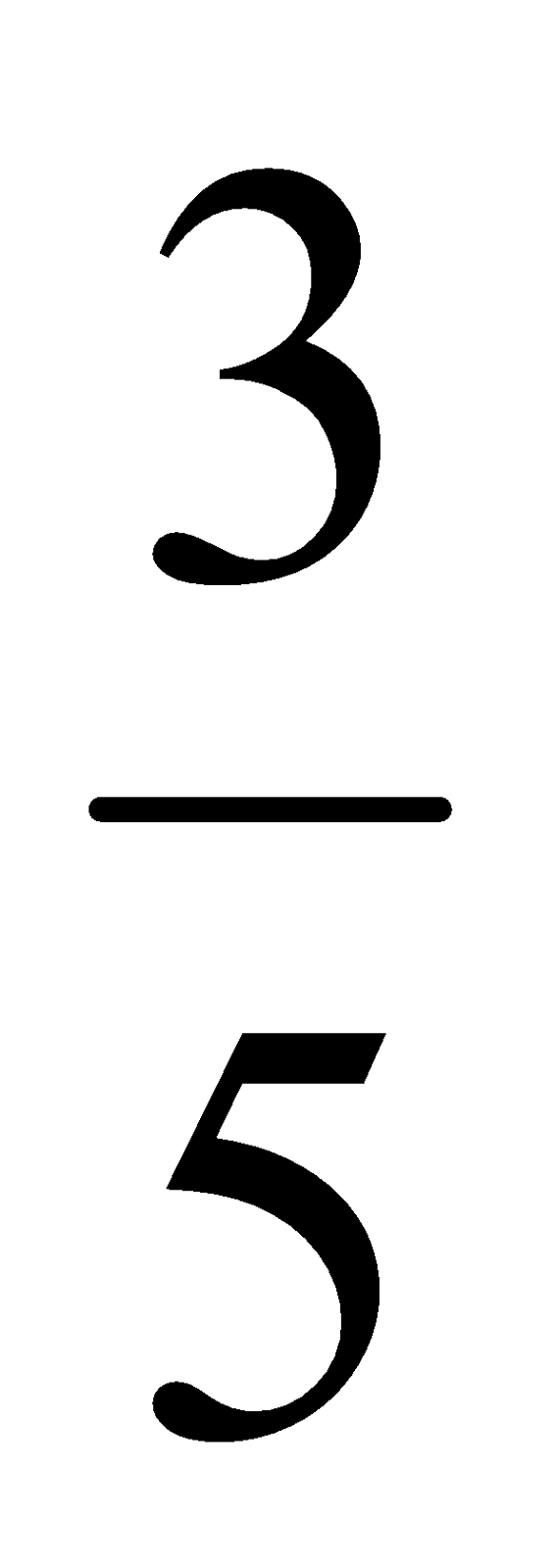 kali tinggi semula begitu dan seterusnya. Jarak lintasan bola sampai berhenti adalah ….
kali tinggi semula begitu dan seterusnya. Jarak lintasan bola sampai berhenti adalah ….
A. 12 meter
B. 20 meter
C. 28 meter
D. 32 meter
E. 40 meter
19. Cermati gambar berikut!
Luas gambar di atas adalah … (  = 3,14 )
= 3,14 )
420 cm2
360 cm2
263 cm2
186 cm2
157 cm2
20. Keliling gambar yang diarsir pada bangun datar di bawah ini adalah....
-
74 cm
80 cm 14 cm
188 cm
668 cm
26 cm
21. Dari
angka 1, 2, 3, …, 7 akan disusun bilangan ganjil bernilai ribuan dengan
tidak ada angka berulang. Banyaknya bilangan yang dapat disusun adalah …
A. 140
B. 360
C. 480
D. 520
E. 840
22. Seorang
siswa diminta mengerjakan 7 dari 10 soal ulangan, tetapi nomor 1 dan 3
harus dikerjakan. Banyaknya pilihan yang dapat diambil siswa adalah ….
A. 21
B. 35
C. 56
D. 70
E. 336
23. Sebuah dadu bersisi 6 dilempar undi satu kali. Berapakah peluang muncul mata dadu kelipatan tiga tidak ganjil?
A. 
B. 
C. 
D. 
E. 
24. Sebuah
kotak berisi 5 bola berwarna merah dan 3 bola berwarna hijau. Jika
diambil 2 bola sekaligus dari kotak itu, maka peluang yang terambil bola
merah dan hijau adalah ….
A. 
B. 
C. 
D. 
E. 
25. Perhatikan gambar di bawah ini.
Pernyataan yang benar pada diagram di atas adalah …
Pendaftar hari keduabelas mencapai jumlah tertinggi.
Jumlah pendaftar hari kesepuluh lebih banyak dibandingkan hari terakhir
Jumlah pendaftar hari kesepuluh mengalami penurunan tertinggi
Jumlah pendaftar hari terakhir lebih banyak dari hari ketujuh
Jumlah pendaftar hari kesebelas lebih banyak dibandingkan hari kedelapan
26. Nilai
rata-rata ulangan matemátika dari 32 siswa ádalah 7. Jika ditambah
nilai dari 8 siswa yang mengikuti ulangan susulan rata-ratanya menjadi
7,1. Rata-rata dari 8 siswa tersebut ádalah ….
A. 7,2
B. 7,3
C. 7,4
D. 7,5
E. 7,6
27. Perhatikan table berikut!
Data
|
Frekuensi
|
50 - 54
55 - 59
60 - 64
65 - 69
70 - 74
75 - 79
80 - 84
|
8
2
3
20
6
15
6
|
Rata-rata hitung dari data pada table di atas adalah ….
68,75
68,92
68,97
69,25
69,40
28 . Modus dari data pada tabel distribusi frekuensi di bawah ini adalah ...
Tinggi Badan
|
Frekuensi
|
150 – 154
155 – 159
160 – 164
165 – 169
170 – 174
175 – 179
|
9
10
6
5
4
2
|
A. 154,2
B. 154,5
C. 155,0
D. 155,5
E. 156,5
29. Simpangan rata-rata dari data 24, 25, 26, 30, 28, 29, adalah ….
A. 1,2
B. 1,6
C. 1,8
D. 2,0
E. 2,2
30. Koefisien variasi dan simpangan baku dari sekumpulan data 3,2% dan 2,4. Rata-rata data tersebut adalah ….
A. 72
B. 74
C. 75
D. 78
E. 80
31. Modal
sebesar Rp6.000.000,00 dibungakan dengan suku bunga tunggal. Berapa
persen suku bunga per tahun apabila modal setelah dibungakan selama 1
tahun 3 bulan menjadi Rp6.450.000,00?
A. 3 %
B. 4 %
C. 5 %
D. 6 %
E. 8 %
32. Seseorang
meminjam sejumlah uang dengan sistem diskonto 12% per tahun. Jika uang
yang ia terima Rp1.840.000,00, maka uang yang harus ia kembalikan
setelah 8 bulan sebesar?
A. Rp2.000.000,00
B. Rp2.400.000,00
C. Rp2.500.000,00
D. Rp2.800.000,00
E. Rp3.000.000,00
33. Pada
awal bulan Desy menabung di bank sebesar Rp500.000,00. Jika bank
memberi suku bunga majemuk sebesar 1,5% per bulan. Dengan bantuan tabel
berikut, maka tabungan Desy setelah satu tahun adalah….
A. Rp580.250,00
n
|
1,5 %
|
10
|
1,1605
|
11
|
1,1779
|
12
|
1,1956
|
B. Rp588.950,00
C. Rp597.800,00
D. Rp598.600,00
E. Rp601.550,00
34. Sebuah
modal setelah dibungakan selama 2,5 tahun dengan suku bunga majemuk
1,5% per triwulan. menjadi Rp8.000.000,00. Dengan bantuan table bunga
berikut, modal sebelumnya adalah ….
n
|
1,5%
|
8
9
10
|
0,8877
0,8746
0,8617
|
A. Rp7.101.600,00
B. Rp7.025.400,00
C. Rp6.996.800,00
D. Rp6.893.600,00
E. Rp6.886.200,00
35. Setiap
akhir bulan bu Santo menyimpan uang di bank sebesar Rp400.000,00
dimulai bulan Juni 2011 dengan suku bunga majemuk 0,25% per bulan.
Dengan bantuan table berikut, berapa besar simpanan bu Santo pada akhir
bulan Oktober 2012 begitu simpanan terakhir disetorkan!
n
|
0,25%
|
16
17
18
|
16,3443
17,3876
18,4336
|
A. Rp6.537.720,00
B. Rp6.937.720,00
C. Rp5.203.290,00
D. Rp5.516.280,00
E. Rp5.530.080,00
36. Setiap
akhir bulan Ajeng mendapat bantuan dari suatu yayasan yang diterima
secara terus menerus sebesar Rp125.000,00. Bantuan tersebut diterima
melalui bank. Apabila Ajeng menghendaki bantuan tersebut diterima
sekaligus di awal bulan pertama dan pihak bank setuju dengan
memperhitungkan suku bunga majemuk 0,5% per bulan. Berapa uang yang
diterima Ajeng?
. A. Rp20.000.000,00
Rp20.125.000,00
Rp25.000.000,00
Rp25.125.000,00
Rp27.125.000,00
37. Perhatikan table pelunasan berikut!
No.
|
Pinjaman Awal Bulan
|
Anuitas
|
………………
|
Sisa Pinjaman
|
|
|
Bunga 3%
|
Angsuran
|
|
1.
|
……………………..
|
Rp150.000,00
|
………………..
|
………………..
|
2.
|
Rp4.800.000,00
|
…………….
|
…………………
|
………………..
|
Sisa pinjaman bulan kedua pada table di atas adalah ….
Rp4.650.000,00
Rp4.594.000,00
Rp4.536.000,00
Rp4.424.000,00
Rp4.415.000,00
38. Suatu
pinjaman sebesar Rp15.000.000,00 akan dilunasi dengan anuitas tahunan
sebesar Rp2.500.000,00. Jika suku bunga majemuk 10% per tahun. Berapakah
bunga pada bulan ketiga?
A. Rp1.500.000,00
B. Rp1.400.000,00
C. Rp1.290.000,00
D. Rp1.260.000,00
E. Rp1.200.000,00
39. Suatu
aktiva setelah dipakai selama 5 tahun mempunyai nilai sisa
Rp8.000.000,00. Jika beban penyusutan setiap tahun Rp2.400.000,00 dengan
metode garis lurus, maka nilai aktiva tersebut adalah ….
A. Rp12.000.000,00
B. Rp15.000.000,00
C. Rp18.000.000,00
D. Rp20.000.000,00
E. Rp25.000.000,00
40. Nilai suatu aktiva Rp25.000.000,00, setelah dipakai selama 5 tahun mempunyai
nilai sisa Rp10.000.000,00 dengan jumlah jam kerja aktiva 25.000 jam.
Jika selama tiga tahun aktiva tersebut sudah bekerja selama 18.000 jam.
Dengan metode satuan jam kerja, maka nilai sisa aktiva setelah tiga
tahun adalah ….
A. Rp10.800.000,00
B. Rp11.200.000,00
C. Rp12.600.000,00
D. Rp13.800.000,00
E. Rp14.200.000,00
KUNCI JAWABAN
D 11. B 21. B 31. D
C 12. A 22. C 32. A
D 13. E 23. A 33. C
B 14. B 24. E 34. D
B 15. A 25. B 35. B
D 16. C 26. D 36. C
E 17. E 27. C 37. B
A 18. D 28. D 38. D
E 19. C 29. D 39. D
C 20. B 30. C 40. E
Terimakasih anda telah membaca artikel tentang Latihan Soal UN Matematika. Jika ingin menduplikasi artikel ini diharapkan anda untuk mencantumkan link https://endah85.blogspot.com/2015/02/latihan-soal-un-matematika.html. Terimakasih atas perhatiannya.